Is the higher order Rosenbrock method worth the effort?

The obvious question that comes to mind is, with the additional rigor involved in the matrix inversion, and sometimes defining the analytical Jacobians for more exact solutions, is the higher order Rosenbrock method worth the effort. The explicit RK method is potentially a much easier algorithm to implement. But does it fare as well as the Rosenbrock method?

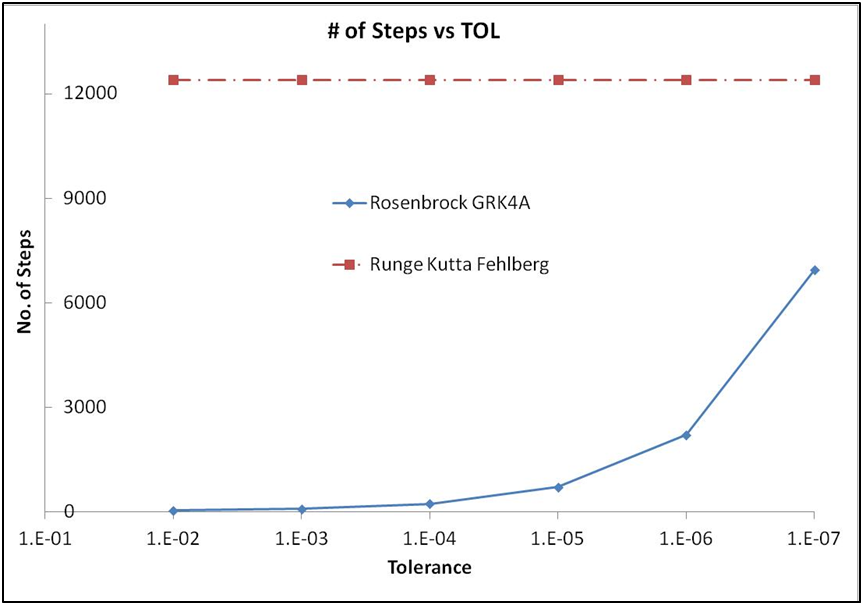
Stiff differential equations are more effectively solved with the Rosenbrock methods. Consider, for example, problem E3 from Enright & Pryce which was solved earlier. With the Rosenbrock-GRK4A coefficients, the solution is obtained from t= 0 to 500, with TOL = 1E-5 in about 715 steps. In contrast, the RK-Fehlberg algorithm takes over 12,400 steps to barely solve for the entire range.

The number of steps as a function of TOL is shown below for GRK4A for the same example. The Rosenbrock method consistently over-performs even with stringent tolerance requirements.