Generalized Runge Kutta Formulation

For RK methods of order 4 and higher, the inter-stage vectors (k’s) can be represented using the following formulation (Atkinson et al, Numerical Solution of ODE’s):

    

The solution at t(n+1) is given by

 

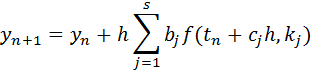
J.C. Butcher (Numerical Methods for ODE’s, 2^nd Edition) invented the “Butcher tableau” methodology of representing the coefficients a(i,j), b(j) and c(j) for the Runge Kutta methods. The general format of such a tableau is

 

 The Butcher tableau for the most popular RK4 method thus becomes:

                                                                                                           

The use of the Butcher tableau, along with the generalized formulation from Atkinson, provides an easy methodology for numerical integration of ODEs.