2-step Euler's method

One technique to improve the stability of the Euler’s method is to use a 2-step approach at each step of integration. That is, given a step size h, one can perform two sub-steps, t(n) to t(n+h/2) followed by t(n+h/2) to t(n+h). Mathematically, this becomes:



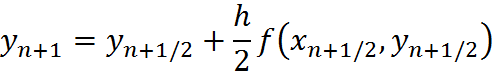
 The algorithm then becomes:
1)    % Define step size (h), initial function y(0), initial time t0, final time tf
2)    nosteps = (tf – t0)/h
3)    for i ← 1 to nosteps

-       Calculate derivative function f[t0,y[i-1]], and
-       y[i*] ← y[i-1] + 0.5*h* f[t0,y[i-1]]
-       t0 ← t0 + h/2
-       Calculate f[t0, y[i*]]
-       y[i] ← y[i*] + 0.5*h* f[t0, y[i*]]
-       t0 ← t0 + h

4)    % Display results

The example from Hairer & Lubich’s report (Numerical solution of ODE’s, source unknown) is a great example to illustrate this concept. The figure below shows the solution of the equation using a 1-step Euler method (with a step size of 0.038), and compares it with a 2-step solution. The 2-step solution has a more “smooth” behavior and hence a more stable. This is evident from the fact that the 2-step approach uses half the step size at each time step for the integration.

 


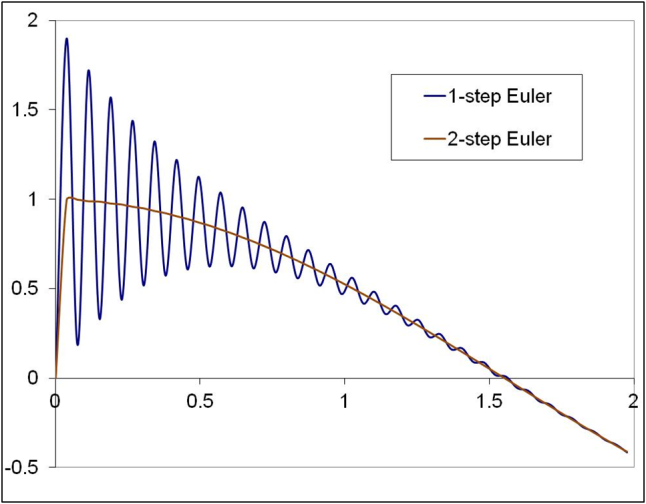
The 2-step Euler serves other practical uses too. Such an approach can be used to estimate the error in the solution (which can prove to be useful if an analytical solution is unknown). Based on this error at a particular step, the 2-step approach can potentially be used to modify the step size for future steps. This would pave way for an adaptive step size approach (contrast this with the existing approach which uses a fixed step size for all time steps).