Two approaches can be used for this iterative process. With a fixed step approach, the future step size for every iteration can be halved from the previous step until convergence. Alternatively, the step size can be adaptively determined using the idea that the error is proportional to the square of the step size (ref. C.W. Gear, Numerical Initial Value Problems in ODE’s, and Prof. Feldman’s notes at www.math.ubc.ca/~feldman/math/vble.pdf).

If the error is greater than TOL, then the new step size for the iteration is
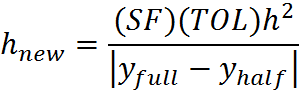
C is the constant of integration. SF is a safety factor (typically 0.9) that is used to ensure the new step does not overshoot the estimate.
The algorithm for adaptive step size Euler’s method can be thusly stated:
1) % Define original step size (h), y_half and y_full, TOL – these are defined as part of the original Euler’s loop.
2) Error = abs(y_half – y_full)
3) Do Until Error <= TOL
- Calculate hnew
- Recalculate y_half and y_full with hnew
- Recalculate y_half and y_full with hnew
4) Proceed to next time step
The example from Prof. Feldman’s notes was used to illustrate the concept. The IVP is:
A TOL of 0.005 was used for the analysis. The solution is shown in the figure below. Although the solutions for both the full and the half steps are practically the same with a 0.005 TOL, an interesting phenomenon can be observed at the circled locations in the figure. Is the “kink” real, or an artifact of the integration process?!
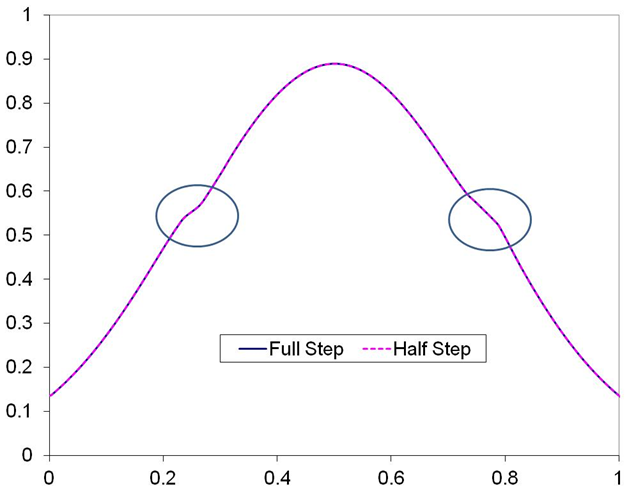
[…] the figure from the variable step-size Euler’s approach. The inconsistencies in the plot at the circled locations are due to this phenomenon of […]
ReplyDelete[…] The difference between the two values of y then serves as an estimate of the error. A variable step algorithm can then be developed based on the error estimate, similar to the one presented for the Euler’s method. […]
ReplyDelete[…] new step. They also suggest bounding the stepsize with a min and max delimiter, as outlined in the Euler’s variable step […]
ReplyDelete