The Euler's Method

Given a differential equation of the form  , a curious mind (the kind of mind that has nothing better to do in life) may wonder how one can go about solving such a DE to produce a variety of colorful numerical results. A simple closed-form analytical solution would obviously be ideal to make things simple. However, let us assume for the moment that an analytical solution either does not exist, or cannot be determined. In most real world cases, this is a perfectly valid assumption. So, how does one go about numerically solving the above differential equation?


Perhaps the simplest of numerical integration techniques is the Euler’s method. The premise of the Euler method is based on the definition of the slope of a curve at a given point from basic calculus.




 

Rearranging the above eqn., one can obtain


 

The newly rearranged equation above represents a method for marching from stage ‘x’ to ‘x+h’, given a value for y’(x) at x=0. In other words, given f(0), one can march along from y(0) with incrementing values of h to obtain a numerical solution for the 1^st order ODE. Thus,


Step 0: f(0) = initial value
Step 1: f(step=1) = f(step=0) + hf’(step=0)
Step 2: f(step=2) = f(step=1) + hf’(step=1)
...

The recursive statements are usually represented in the following format:

 

The algorithm for Euler's method of numerical integration can be summarized as follows:


1) % Define step size (h), initial function y(0), initial time t0, final time tf
2) nosteps = (tf – t0)/h
3) for i ← 1 to nosteps

- Calculate derivative function f[t0,y[i]]
- y[i] ← y[i-1] + h*f[x,y]
- t0 ← t0 + h

4) % Display results

To illustrate the procedure, the Euler’s method was applied to the following initial value problem (Butcher, Numerical methods for ordinary differential equations, 201(a)) with a step size of 0.001.

 

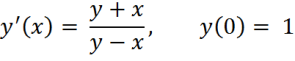
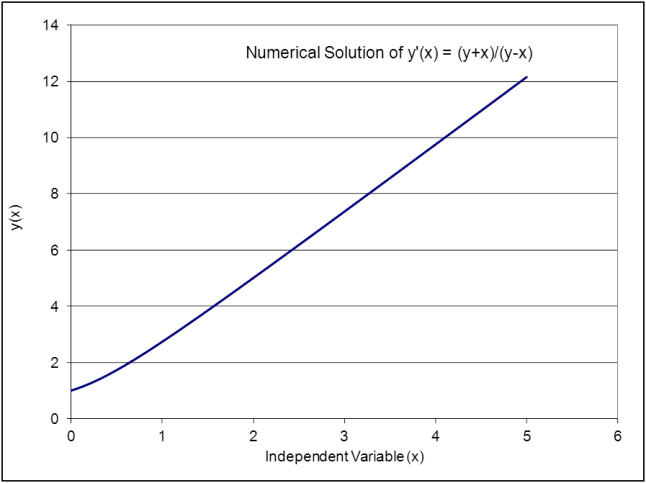
 The result of the integrated function is plotted in fig. (1).