Direction Fields serve as a valuable tool to visualize differential equations. In the simplest form, the derivative of a function at a specific location, say (x,y), is the slope of the function at that point. Consider, for example, the simple DE
y’ = y (t), with boundary condition of y(0) = 1
The above equation can be easily solved using well known techniques to obtain an analytical solution. Instead, let us attempt to plot the slope (i.e., y’) at various instances of time t, for various values of y. One such plot is shown below in Fig. (1). The direction fields provide a visual clue to the form of the solution for the initial value problem. Also plotted in Fig. 1 is the analytical solution (solid brown line).
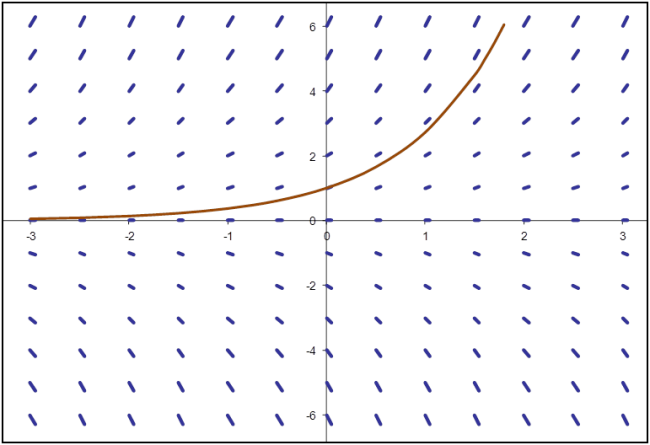
Fig 1: Direction fields for y’ = y, with analytical solution y(t) = exp(t)
A variety of curves (i.e., solutions to the DE) can be visualized from Fig. 1. Each of these curves corresponds to their equivalent initial value problems. The analytical solution shown in Fig. 1 is one case of the initial value problem, where y(0)=1. Using the direction fields, one can visualize the form of the solution for various initial values. For a negative intercept on the ordinate (i.e., initial value problems with y(0) < 0), the form of the solution would be a mirror image of the solid brown line about the abscissa. This is visually evident from the direction fields shown for times t < 0 in Fig. 1.
Fig. 2 shows another example of a direction field plotted for the following 1st order DE (Atkinson et al, Numerical Solution of Ordinary Differential Equations, problem 1(a))
y’ = -y(t) + sin(t) + cos(t), y(0) = 1
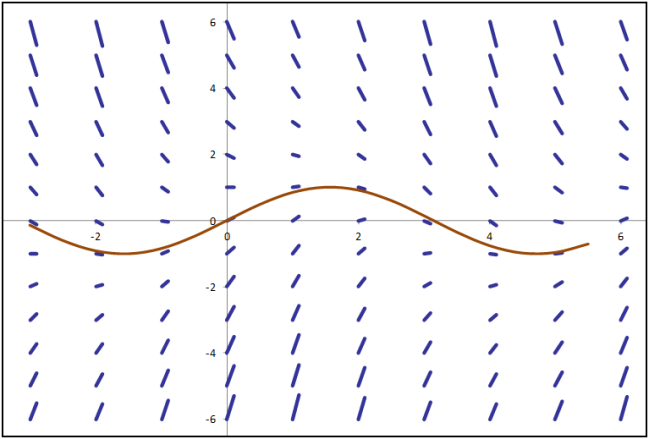
Fig. 2: Direction fields for y’ = -y + sin(t) + cos(t), with analytical solution
Great start! Keep posting :)
ReplyDelete