Pitfalls with the variable step Euler method

While the variable step size algorithm has its advantages (of potentially reducing the number of steps required to perform the integration based on the tolerance, compared to a fixed step algorithm), one needs to be extremely vigilant of overshoots in steps.

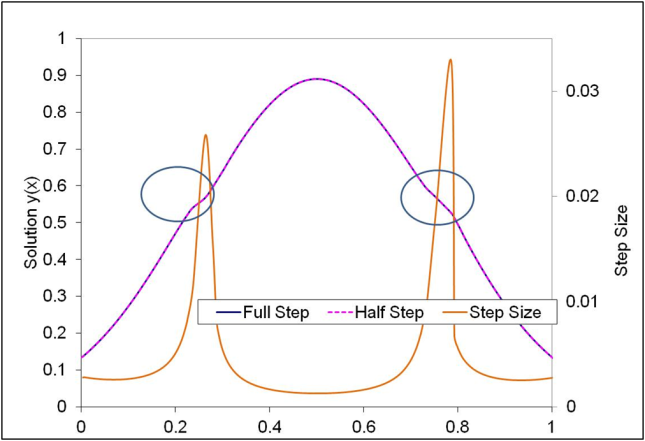
Consider the figure from the variable step-size Euler’s approach. The inconsistencies in the plot at the circled locations are due to this phenomenon of overshoot in the step-size. The figure below shows the step-size versus time for the same problem. The overshoots in step-sizes occur at the exact instances where the “discontinuities” show up in the solution of y(x).

  

To avoid such discontinuities, P. Kaps & P. Rentrop (Generalized Runge Kutta Methods of Order Four with Stepsize Control for Stiff ODE’s, Numerical Mathematics, Vol. 33, Issue 1, pp 55-68, 1979) suggest bounding the steps using the following approach:

If hnew > A * hold, then hnew = A * hold
If hnew < B * hold, then hnew = B * hold

where A and B are positive constants, A > 1 and B < 1. Kaps & Rentrop quite simply suggest that A and B are chosen based on experience! Intuitively, the aim is to ensure that the step-sizes do not get too large. Conservative values for A and B can be 1.2 and 0.8, thus bounding the new step sizes to between 0.8 and 1.2 times the old step size.

The figure below shows the solution with such a bounded step size implementation, using constants A=1.1 and B=0.9.

 

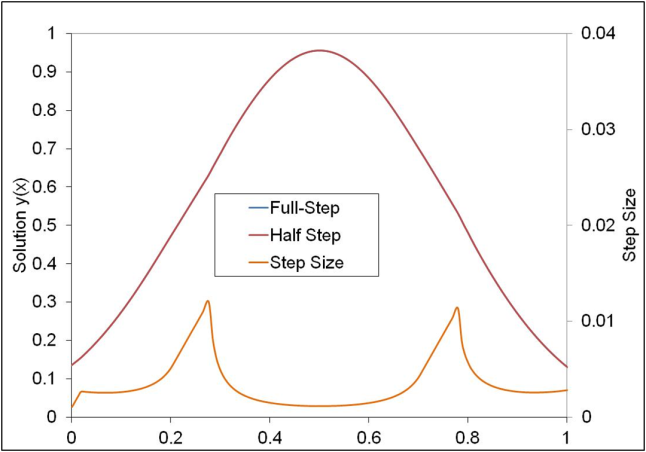
 How does one go about choosing A & B for all cases? Perhaps there are better estimates for determining step sizes out there that can simplify the process? Or perhaps it is time to advance to higher order methods in numerical integration?!