Euler’s method part 2- Does it work for all cases?

Let us now consider applying the Euler’s method to the problem described in Curtiss & Hirschfelder (Integration of stiff equations, Proc. of the Natl. Acad. Of Sciences, 1952, Vol. 38, pp 235-243). This is the first order DE described by the equation

 


The results of the numerical integration are shown in fig. (1) for various step sizes ‘h’, for the initial value y(0)= 1.

 

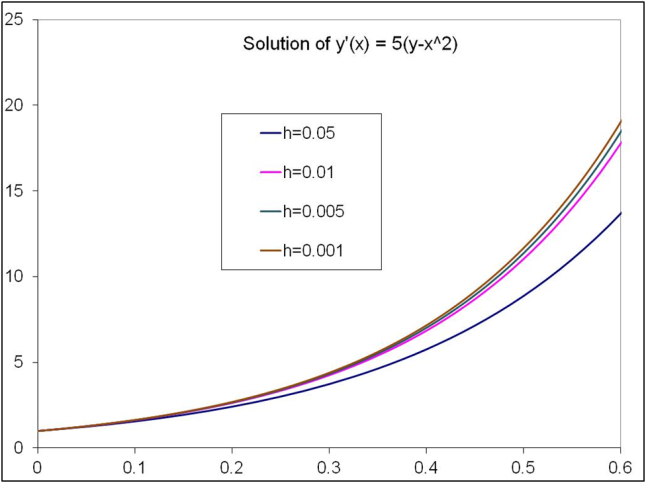
 Fig. (1): Solution of a quadratic equation for various 'h' values

Clearly the numerical solution changes for various step sizes. So which of the solution curves in fig. (1) is the “correct” solution? The simplistic marching scheme presented by the Euler’s method is clearly not “stable” for all values of step sizes. In other words, the Euler’s method does not converge to a solution for any value of ‘h’. A minimum value of ‘h’ is thus required for the numerical solutions to converge. Note on fig. (1) that the solutions tend to converge as ‘h’ decreases.


The quest for a numerical integration procedure for an ODE is thus to come up with one that is stable for any and every value of ‘h’. The forward-Euler method clearly does not appear to meet this criteria for certain types of DE’s.


To illustrate the point, the solution of the equation

 

 from Ernst Hairer & Christian Lubich, (paper titled Numerical Solution of Ordinary Differential Equations, reference unknown) for various values of ‘h’ is shown in fig. (2).

 

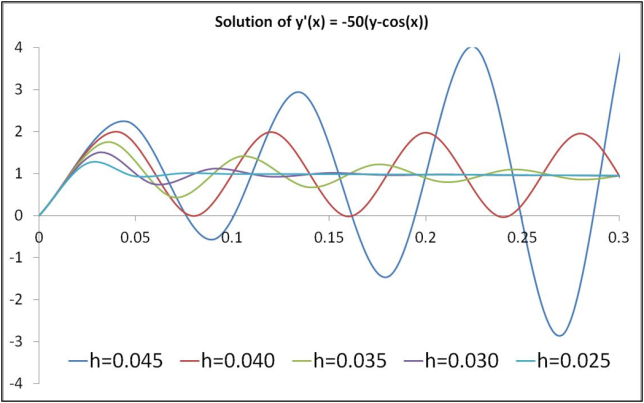
Fig (2): Solution for y'(x) = -50(y-cosx)

These two examples clearly illustrate the need for numerical integration techniques that can converge to a solution independent of the step size ‘h’.