The backward Euler's method

The examples in the previous post suggested the importance of step-size ‘h’ for numerical integration, and how improper choices of ‘h’ may lead to a divergent solution. The Euler’s method presented in the former post, as indicated earlier, marched from time tn to tn+1 using the knowledge of the solution at time tn. This method is also known as the Forward Euler, since it marches forward in time.

The forward Euler at time tn uses the derivative at tn to march to tn+1. Instead, if the derivative is obtained at time tn+1, the method becomes the Backward Euler. Mathematically, it is represented by the following equation:



Since the function y(x) appears on both sides of the equation, one can no longer simply march forward between time steps. Rather, one needs to perform an iterative root-finding algorithm to determine y(x) at each time step

A simplified algorithm for the Backward-Euler can be summarized as follows:

1)    % Define step size (h), initial function y(0), initial time t0, final time tf, eps
2)    nosteps = (tf – t0)/h
3)    for i ← 1 to nosteps

- Calculate derivative function f[t0,y[i]]
- Iterate until y[i] – (y[i-1] + h*f[x(i), y(i)]) < eps
- t0 ← t0 + h

4)    % Display results

‘eps’ is a user-specified tolerance value for the root-solver. The solver iterates until the equation at each time step is less than ‘eps’. The value that satisfies this condition is the numerical solution at that time. The iteration can be performed using any root-finding algorithm like the Bisection or the Newton-Raphson method. A modified form of the subroutine ‘rtbis’ adapted from Numerical Recipes, (The art of scientific computing, Press et al, 2^nd ed.) was used for this exercise.

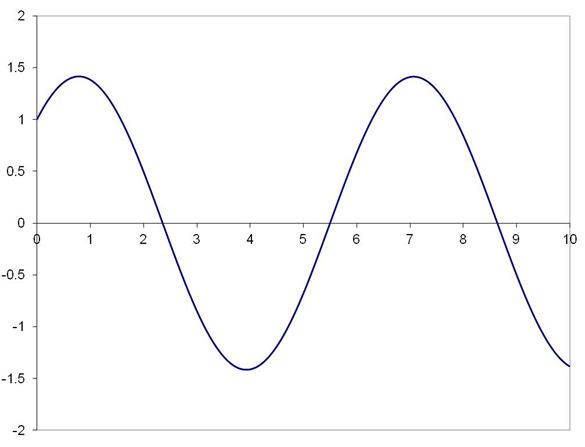
The Backward Euler’s method was applied to the following problem (Atkinson et al, Numerical Solution of Ordinary Differential Equations, Eg. 5.8).

 

 The solution is shown in fig. 1.