4th order Runge Kutta Method

The classical higher order Runge Kutta method of order 4 involves four calculations at each time step to advance with the numerical solution. The steps of integration are summarized as:

 






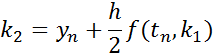
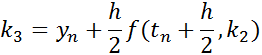
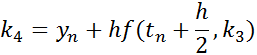
Using k1-k4 from the above, the next step is calculated as:

 

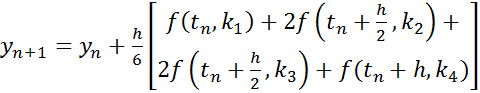
 The algorithm for the RK4 method can be summarized as:

1)    % Define step size (h), initial function y(0), initial time t0, final time tf
2)    nosteps = (tf – t0)/h
3)    for i ← 1 to nosteps

-       Calculate derivative function f[t0,y[i-1]]
-       k1 ← f[t0,y[i-1]]
-       Calculate f[t0,k1]
-       k2 ← y[i-1] + 0.5*h*f[t0,k1]
-       t0i ← t0 + 0.5*h
-       Calculate f[t0,k2]
-       k3 ← y[i-1] + 0.5*h*f[t0i,k2]
-       k4 ← y[i-1] + h*f[t0i,k3]
-       y[i] ← y[i-1] + (h/6)*{f[t0,k1] + 2 f[t0i,k2] + 2 f[t0i,k3] + f[t0+h,k4]
-       t0 ← t0 + h

4)    Display results