Coupled spring-mass-damper systems

By adding some damping to the spring-mass system, a new set of patterns start to emerge for the phase plots and the relative displacements.

The following values were used for the simulation:

The initial values used were:

 

The numerical integration was performed using the Rosenbrock triple.

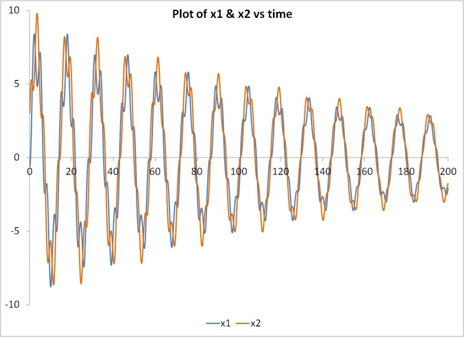
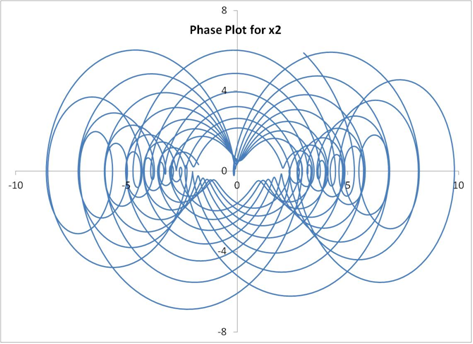
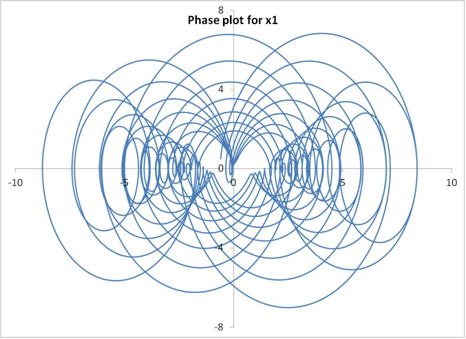
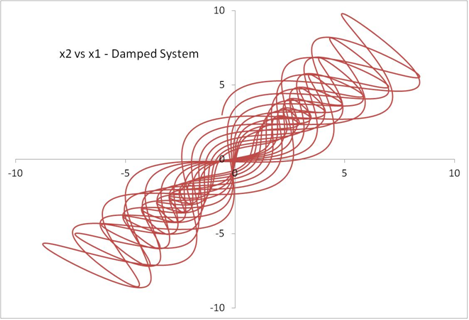
A plot of displacement versus time is also shown below to better understand the physics of the motion. As expected, the oscillations tend to die down with time in the presence of viscous damping. Although the motion appears periodic and linear, it is not! And this is evident from the relative displacement plot. By merely adding damping to the system, a new pattern has emerged.