Coupled spring-mass systems

Is it possible that one does not need to resort to something as complex as a pendulum motion to create such “pretty flowers”? Can one create more such mathematical patterns by looking at simpler systems?

The motion of the pendulum is certainly complex in the real world. However, if one were to observe a ball bobbing up and down on the inner surface sphere as it traverses its motion, one may not be as “fascinated” with the actual motion, I believe. (Replace the ball with a motorcyclist and the sphere with a cage, and the motion of the motorcyclist strikes awe in every viewer, mainly due to the involvement of a human element). This is partly due to the fact that one cannot completely keep track of the entire path traversed by the mass over a substantial period of time, but rather be able to see the mass only at each instant of time. The floral pattern is nothing but a visual representation of the path traveled by the pendulum from start to finish.

Two-degree of freedom systems with two masses connected by springs (and dampers) are a very common example taught in undergraduate mechanics courses. The equations of motion for such systems can be quite easily derived from first principles using Newton’s laws. A generalized form of the ODE’s for such a 2-DOF mass-spring-damper system is given below:





The above ODE’s are mathematically coupled, with each equation involving both variables x1 and x2. One can quite easily solve these systems of equations both analytically and numerically to obtain the position of the two masses as a function of time.

Fay & Graham (Coupled Spring Equations, International Journal of Mathematical Education in Science and Technology, 2003) present a series of examples of such coupled-spring systems. The following values were used to simulate the above equations, which were numerically integrated using the Rosenbrock triple:



The initial values used were:



The solutions for the undamped system (ie., C1=C2=0) are shown below. The phase plot shows velocity as a function of displacement for each of the masses.




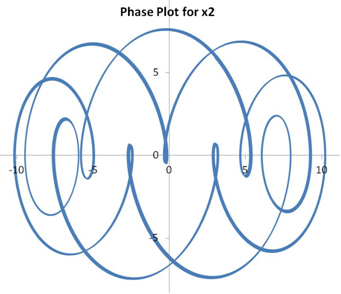
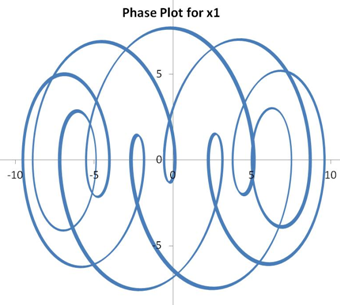
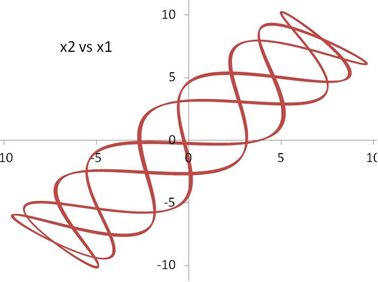
The plot of x2 vs x1 merely represents the motion of the two masses relative to each other, which would otherwise be impossible to visualize in the real world.