The Rosenbrock Method

The use of Jacobians allows for a step-wise formulation of the implicit RK methods as indicated earlier. A natural progression that arises from such Jacobian-methods is the higher order semi-implicit RK methods, which are more commonly referred to as the Rosenbrock methods.

In 1963, H.H. Rosenbrock (Some general implicit processes for the numerical solution of differential equations. Computer J., vol. 5, pp. 329-330) first presented such a methodology. The general format for the Rosenbrock methods is shown below:





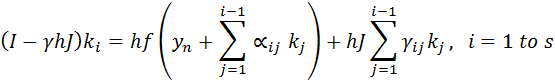
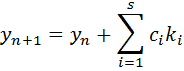
With  , the above equations reduce to the one-stage semi-implicit formulation.



Rosenbrock methods are sometimes referred to as higher order RK methods (ref: Butcher, Numerical Methods for ODEs) since it follows the step-wise implementation of implicit Runge Kutta algorithms, while avoiding the Newton iterations at each step. The superior performance of Rosenbrock algorithms comes into play while solving stiff differential equations.