How does a partial derivative differ from its “impartial” counterpart? A partial derivative is one in which the dependent variable is differentiated with respect to only one of the other variables. Partial derivatives bring in the concept of dimensionality in a real world problem. Heat transfer problems in Mechanical Engineering are a good intuitive example.
Mathematically, let us assume a function
Here, y is a function of x and y. A normal derivative is usually with respect to x (assuming x is the independent variable), while the partial derivative is with respect to y. In the above case, the partial derivative, or the Jacobian of f with respect to y is
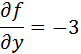
The Jacobian of a function that has multiple dependent variables is thus a matrix of partial derivatives. For example, if f is a function defined by
then the partial derivatives are
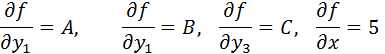
Following the above logic, the Jacobian matrix for a series of ODE’s can be represented as follows:
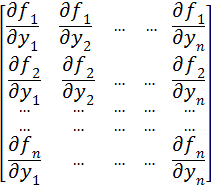
[…] inversion can be performed by using the LU-decomposition followed by the LU-back substitution. The Jacobians can be either defined analytically or computed numerically. The analytical definitions are […]
ReplyDelete[…] use of Jacobians allows for a step-wise formulation of the implicit RK methods as indicated earlier. A natural […]
ReplyDelete