The Brusselator Problem

The Brusselator is a class of ODE’s that describe the autocatalytic reaction. The ODE’s that define the Brusselator as presented in Hairer et al (Numerical Solution of ODEs, Vol 1, Non Stiff Equations) are:

    

 

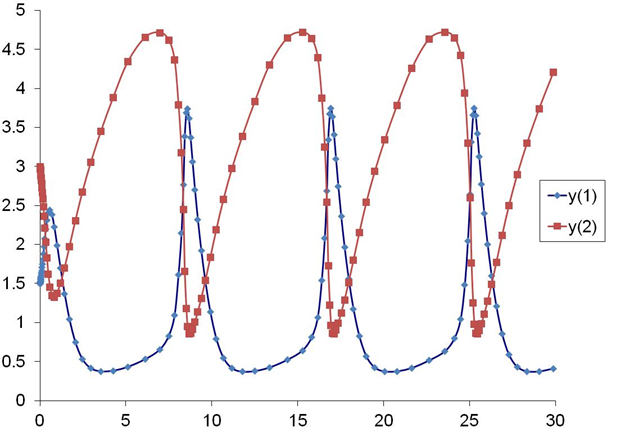
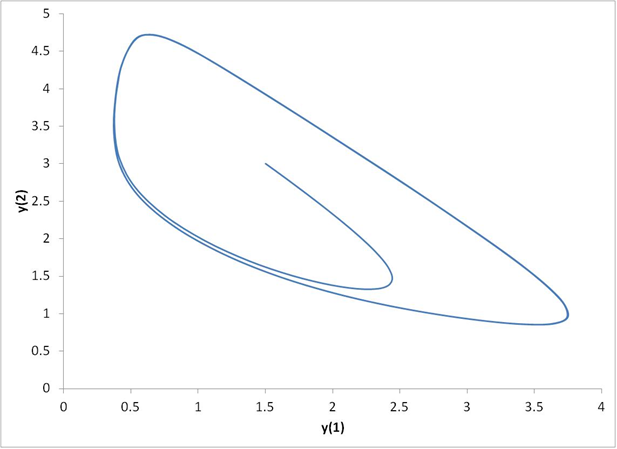
with initial values y1(0)=1.5 and y2(0)=3. The RK-Merson method with the Kaps & Rentrop variable step size algorithm was used to solve the Brusselator problem. An initial step size of 0.001 with a TOL of 0.001 was used.

 The results are shown below. The first figure shows the solutions of y1 and y2 as a function of x. The power of the variable step size is evident from the “dots” in the figure. Extremely small steps are required to initiate the numerical process close to start (at t=0), while fairly generous step sizes can be used as the integration progresses along. Had a fixed step size algorithm been used for the Brusselator, the step size would have to be small all along to avoid numerical instabilities, and thus increases the computation cost significantly.