So, how does one avoid iterations and yet be able to solve the Backward Euler’s method? Press et al (Press, Teukolsky, Vetterling & Flannery, Numerical Recipes, The Art of Scientific Computing) suggest using a linearized form of the equation to represent the derivative f(yn+1). Using the principles of basic calculus,
The above representation introduces the partial derivative on the right hand side. Using this formulation and re-arranging the terms, the Backward Euler becomes:
For simple ODE’s that have just one equation, the above semi-implicit form can be easily solved by dividing the equation with the term in the square brackets, and then marching sequentially from one step to the next. The simplified formulation then becomes:
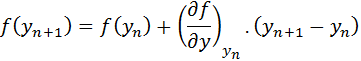

[…] matrix formulation of the semi-implicit methods, as indicated earlier, has the advantage of avoiding an iterative procedure to converge at a solution. However, the […]
ReplyDelete