Kaps-Rentrop’s Variable Step Size Procedure

The need for a variable stepsize control becomes evident when solving a series of ODE’s that have varying settling times for the solution. The requirement for stepsize is limited by the variable that has the shortest settling time, while the small step may be an over kill for the variables with slower settling times. Press et al (Numerical Recipes, The Art of Scientific Computing) very beautifully state that “many small steps should tiptoe through treacherous terrain, while a few great strides should speed through smooth uninteresting countryside”.

P. Kaps & P. Rentrop (Generalized Runge Kutta Methods of Order Four With Stepsize Control for Stiff ODE’s, Numerical Mathematics, vol. 33, 1979, pp. 55-68) have suggested the following stepsize control for adaptive steps in the integration of ODE’s.

Error estimation (and control) is performed by using two separate calculations with coefficients from the Butcher table as described in the Merson’s method. Having calculated y(n+1) and ycap(n+1),

1-      Define a suitable scaling factor

2-      Calculate the local Error estimate, EST 

 

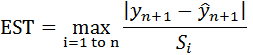
 3-      Given a user supplied tolerance TOL, the new step size can be calculated as

 

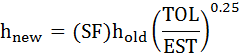
 4-      The following algorithm can then be used for stepsize control:

 Do Until EST <= TOL

-       Calculate hnew
-       Recalculate y(n+1) and ycap(n+1) with hnew

At each stage of the iterative process, hnew is not accepted until EST<=TOL. hnew is progressively reduced in size until EST<=TOL. Once this condition is met, the same formulation for hnew is used one more time to advance to the next step.

Kaps & Rentrop suggest C=1 for the scaling vector, and a safety factor SF = 0.9 to conservatively guess on the new step. They also suggest bounding the stepsize with a min and max delimiter, as outlined in the Euler’s variable step algorithm.