More on the Semi-Implicit method

The matrix formulation of the semi-implicit methods, as indicated earlier, has the advantage of avoiding an iterative procedure to converge at a solution. However, the reformulation introduces two additional complications – matrix inversion and Jacobian.

Matrix inversion can be performed by using the LU-decomposition followed by the LU-back substitution. The Jacobians can be either defined analytically or computed numerically. The analytical definitions are obviously preferred so as to avoid any numerical approximation errors with the computation, with the caveat that analytical definitions can become a little tedious to program.

Yet another generalized representation of the semi-implicit method can be stated as follows:





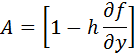
The above representation tends to look more like the generalized RK methods, with the obvious exception of the ‘A’ matrix and the Jacobians!