Wednesday, June 18, 2014

The Modified Rosenbrock Triple

Shampine & Reichelt (The Matlab ODE Suite) point out that the W-formulas can go “badly wrong when solving problems with solutions that exhibit very sharp changes”, especially within each time step. They propose a modified Rosenbrock Triple that advances between time steps. The Rosenbrock Triple is presented below, but re-written in a format that is scaled and conditioned.
New Picture (1)

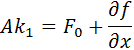
        New Picture (2)
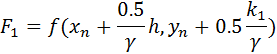
 New Picture (3)

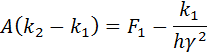
 New Picture (4)

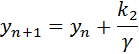
 New Picture (5)

 The error estimate is given by:
 New Picture (6)

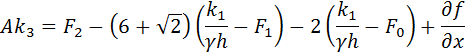
 New Picture (7)

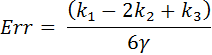
 New Picture (8)

For a successful step, F2 for the completed step is the same as F0 for the next step. Shampine & Reichelt refer to it the “First Same As Last” formula, or FSAL.

The implementation of the Rosenbrock Triple is fairly straight-forward, as is obvious from the one-step formulation above. The matrix inversion in the form of LU decomposition is performed once, and the ki’s are calculated by LU back substitutions.
Posted by at
Labels: , , ,

3 comments:

  1. The 3-body orbit problem | A Handful Of Numerical Integration TechniquesJune 25, 2014 at 4:05 PM

    […] Rosenbrock Triple was employed to solve the above equations. A plot of y2 vs y1 is shown […]

    ReplyDelete
  2. The Spherical Pendulum | A Handful Of Numerical Integration TechniquesJune 27, 2014 at 3:49 AM

    […] The initial conditions of Hairer, Norsett and Wanner were used with the above equations, and were solved using the Rosenbrock Triple. […]

    ReplyDelete
  3. Coupled spring-mass systems | A Handful Of Numerical Integration TechniquesJune 28, 2014 at 4:18 PM

    […] values were used to simulate the above equations, which were numerically integrated using the Rosenbrock […]

    ReplyDelete

Subscribe to: Post Comments (Atom)