Generalized Runge Kutta Formulation

For RK methods of order 4 and higher, the inter-stage vectors (k’s) can be represented using the following formulation (Atkinson et al, Numerical Solution of ODE’s):

    

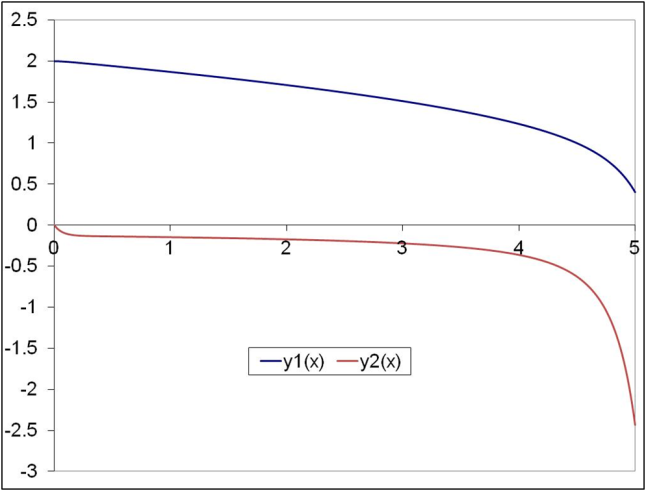
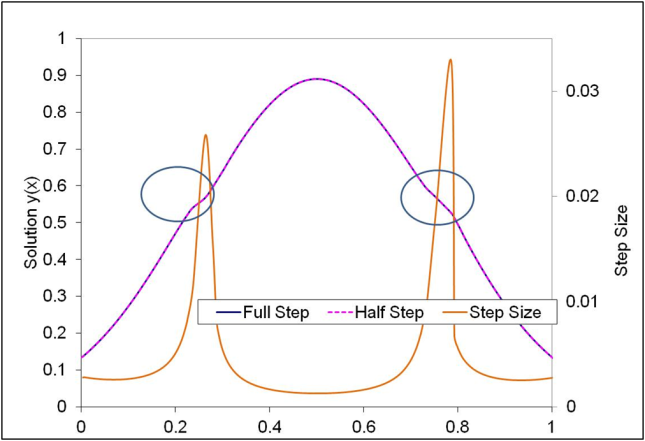
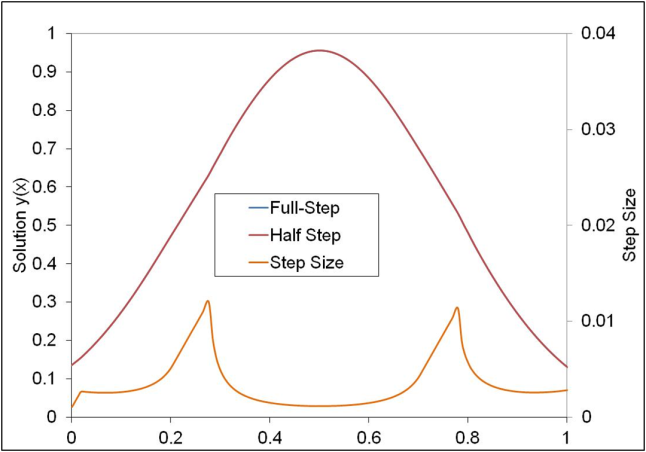
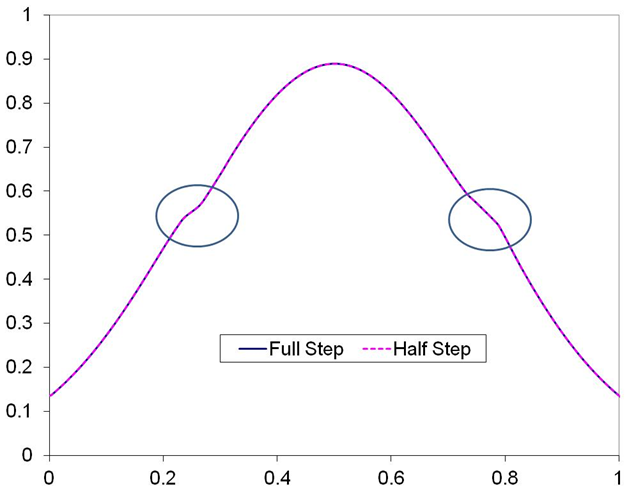
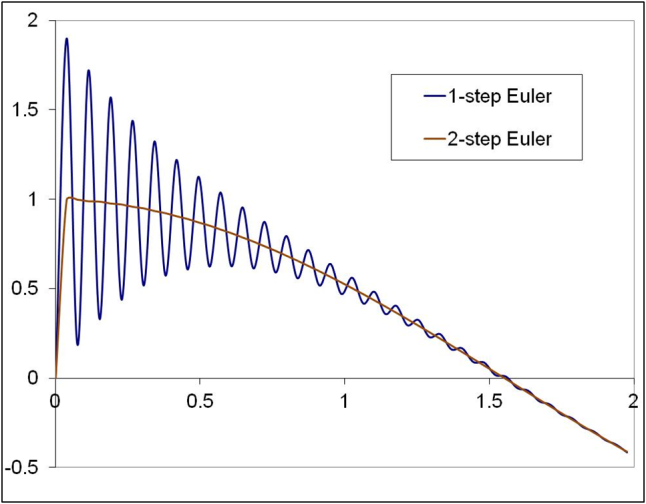
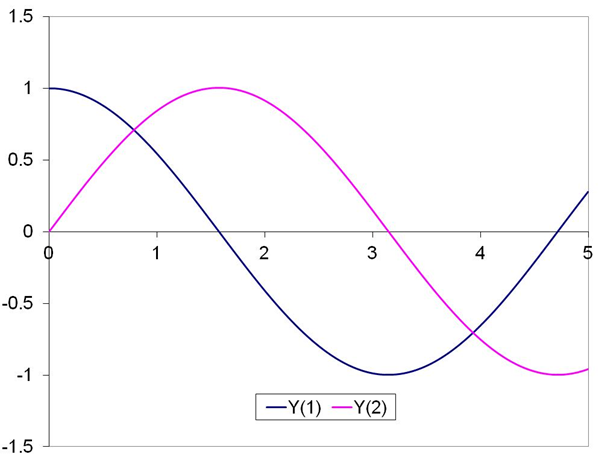
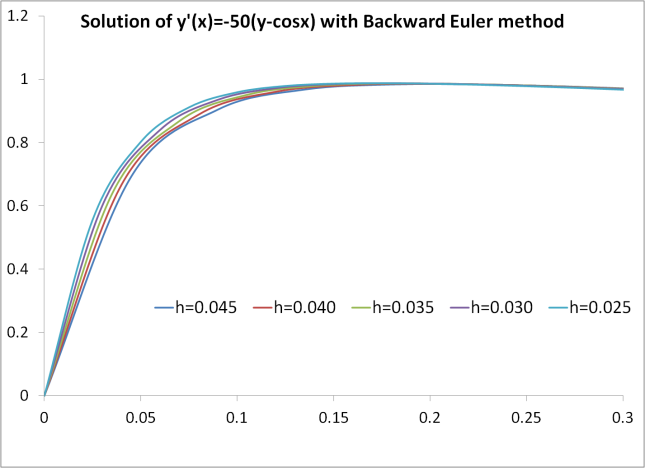
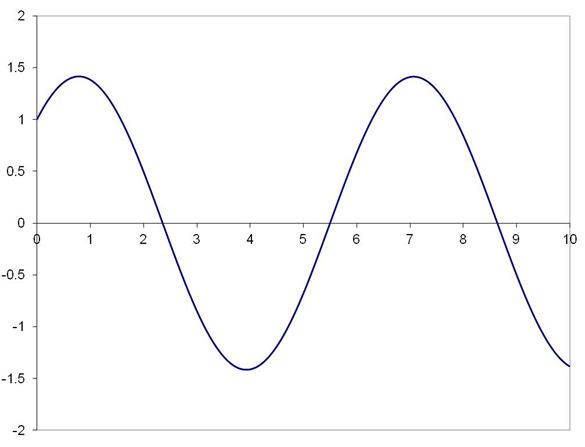
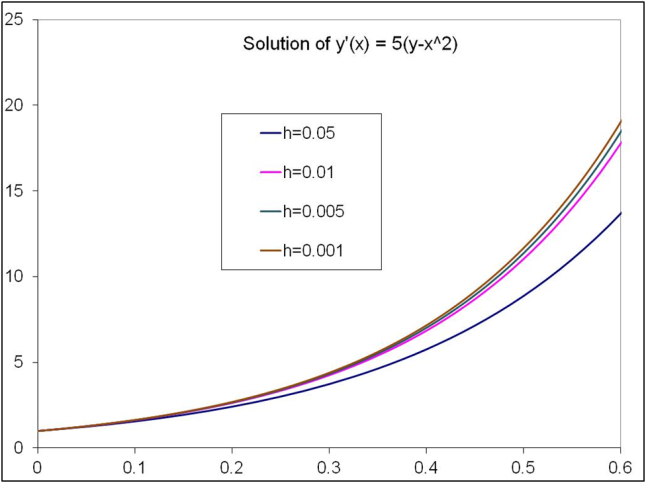
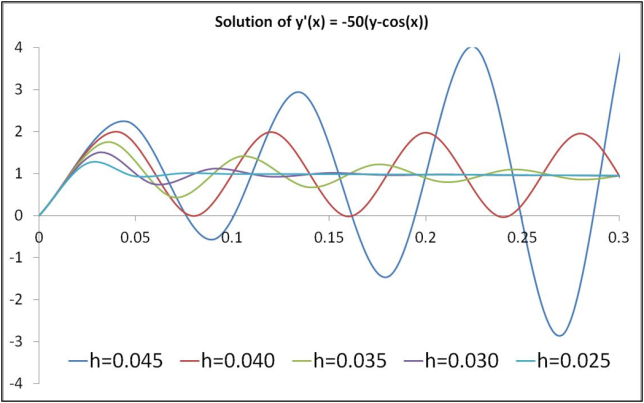
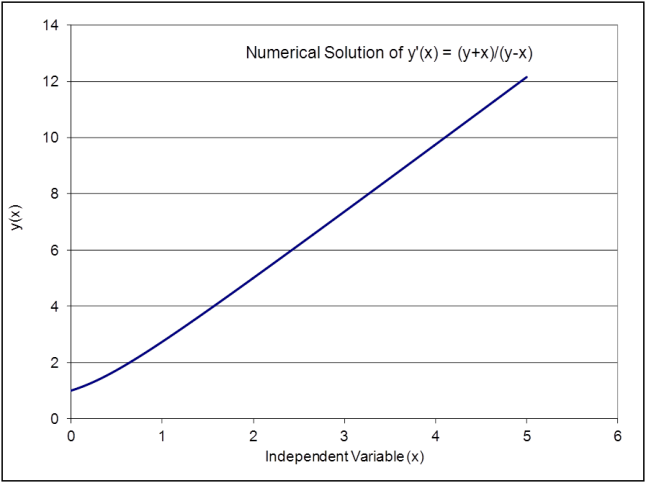
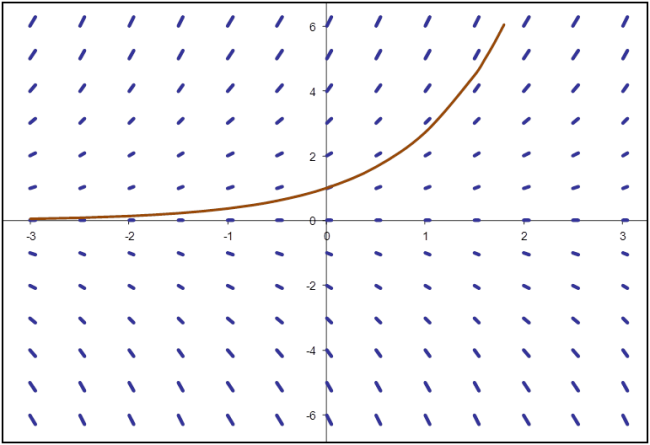
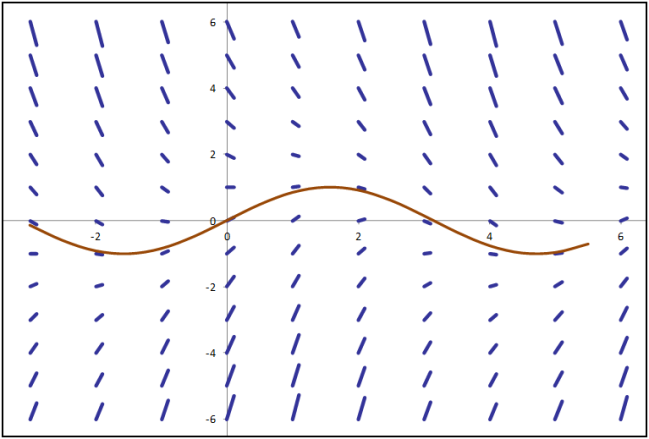
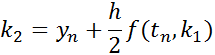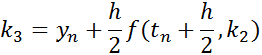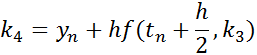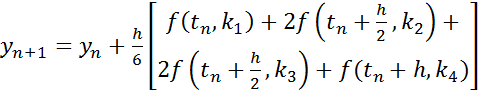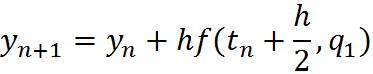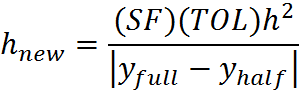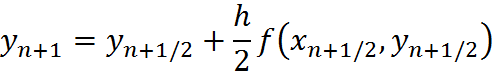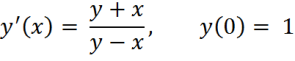The solution at t(n+1) is given by

 

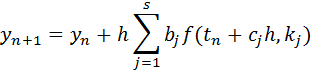
J.C. Butcher (Numerical Methods for ODE’s, 2^nd Edition) invented the “Butcher tableau” methodology of representing the coefficients a(i,j), b(j) and c(j) for the Runge Kutta methods. The general format of such a tableau is

 

 The Butcher tableau for the most popular RK4 method thus becomes:

                                                                                                           

The use of the Butcher tableau, along with the generalized formulation from Atkinson, provides an easy methodology for numerical integration of ODEs.

Runge Kutta 4 - A Numerical Example

Oscillations and vibrations of structural elements are commonly represented as a 2^nd order ODE (derived from Newton’s law). In his paper, Piche (An L-stable Rosenbrock Algorithm for Step-By-Step Time Integration in Structural Mechanics, Computational Methods in Applied Engrg., Vol 126, 1995, pp 343-354) presents one such example of a two-degree of freedom mass-spring-damper system with the following ODEs:

 
with the initial values and constants defined as:

 

Second order ODE’s can be converted to first order ones by substituting equivalent expressions for the first order ones. For example, the above expression is based on Newton’s law, where y1 and y2 represent the motion of the system. The first derivative of displacement is velocity, and the first derivative of velocity is acceleration. Thus, each equation above gets split up into two first order eqns. as shown below:

 



A similar substitution is performed for the other equation also, thus resulting in four 1^st order ODE’s. A numerical integration scheme can then used to solve for y1, v1, y2 and v2.

The RK4 method was used to solve these equations with a step-size of 0.001, and the results for y1 and y2 are shown below.

 

4th order Runge Kutta Method

The classical higher order Runge Kutta method of order 4 involves four calculations at each time step to advance with the numerical solution. The steps of integration are summarized as:

 






Using k1-k4 from the above, the next step is calculated as:

 

 The algorithm for the RK4 method can be summarized as:

1)    % Define step size (h), initial function y(0), initial time t0, final time tf
2)    nosteps = (tf – t0)/h
3)    for i ← 1 to nosteps

-       Calculate derivative function f[t0,y[i-1]]
-       k1 ← f[t0,y[i-1]]
-       Calculate f[t0,k1]
-       k2 ← y[i-1] + 0.5*h*f[t0,k1]
-       t0i ← t0 + 0.5*h
-       Calculate f[t0,k2]
-       k3 ← y[i-1] + 0.5*h*f[t0i,k2]
-       k4 ← y[i-1] + h*f[t0i,k3]
-       y[i] ← y[i-1] + (h/6)*{f[t0,k1] + 2 f[t0i,k2] + 2 f[t0i,k3] + f[t0+h,k4]
-       t0 ← t0 + h

4)    Display results

2-Step Runge Kutta - Example

The 2-step RK method is pretty much the same as the Euler’s method performed with two time steps. The 2-step RK method was used to solve the problem E2 from W.H. Enright & J.D. Pryce (Two Fortran packages for assessing initial value methods, ACM Trans. On Mathematical Software, Vol. 13, No. 1, 1987, pp 1-27). This is the series of equations defined by

 

 

 with y1(0)=2, y2(0)=0. The result is shown below for a step size 0.005.

 

Higher Order Integration Methods

The Euler’s methods (both forward and backward) are single step methods, as is evident from the formulation. An improved solution for ODE’s can be obtained from higher order methods. A series of formulations known as the Runge-Kutta (RK) techniques fall under the higher order methods. The RK methods involve multiple steps at each time instant to move from t(n) to t(n+1).

The simplest of RK methods is the 2-step RK solver. At each time step t(n), given y(n), the solution to advance to y(n+1) is:

  



The RK2 method from the above equations can be quite easily implemented for fixed step size integration. The algorithm can be summarized as:

1)    % Define step size (h), initial function y(0), initial time t0, final time tf
2)    nosteps = (tf – t0)/h
3)    for i ← 1 to nosteps

-       Calculate derivative function f[t0,y[i-1]]
-       q1 ← y[i-1] + 0.5*h* f[t0,y[i-1]]
-       t0 ← t0 + 0.5*h
-       Calculate f[t0,q1]
-       y[i] ← y[i-1] + h*f[t0,q1]
-       t0 ← t0 + h

4)    Display results

Pitfalls with the variable step Euler method

While the variable step size algorithm has its advantages (of potentially reducing the number of steps required to perform the integration based on the tolerance, compared to a fixed step algorithm), one needs to be extremely vigilant of overshoots in steps.

Consider the figure from the variable step-size Euler’s approach. The inconsistencies in the plot at the circled locations are due to this phenomenon of overshoot in the step-size. The figure below shows the step-size versus time for the same problem. The overshoots in step-sizes occur at the exact instances where the “discontinuities” show up in the solution of y(x).

  

To avoid such discontinuities, P. Kaps & P. Rentrop (Generalized Runge Kutta Methods of Order Four with Stepsize Control for Stiff ODE’s, Numerical Mathematics, Vol. 33, Issue 1, pp 55-68, 1979) suggest bounding the steps using the following approach:

If hnew > A * hold, then hnew = A * hold
If hnew < B * hold, then hnew = B * hold

where A and B are positive constants, A > 1 and B < 1. Kaps & Rentrop quite simply suggest that A and B are chosen based on experience! Intuitively, the aim is to ensure that the step-sizes do not get too large. Conservative values for A and B can be 1.2 and 0.8, thus bounding the new step sizes to between 0.8 and 1.2 times the old step size.

The figure below shows the solution with such a bounded step size implementation, using constants A=1.1 and B=0.9.

 

 How does one go about choosing A & B for all cases? Perhaps there are better estimates for determining step sizes out there that can simplify the process? Or perhaps it is time to advance to higher order methods in numerical integration?!

Adaptive step-size for Euler's method

The error in the numerical estimate of the Euler’s method can be determined by performing a 1-step and 2-step integration at each time step. The absolute difference between the full-step and the two-half-step values at each time step then becomes the error estimate. Using this error estimate, iterations can be performed until the error is less than a user specified tolerance (TOL).

Two approaches can be used for this iterative process. With a fixed step approach, the future step size for every iteration can be halved from the previous step until convergence. Alternatively, the step size can be adaptively determined using the idea that the error is proportional to the square of the step size (ref. C.W. Gear, Numerical Initial Value Problems in ODE’s, and Prof. Feldman’s notes at www.math.ubc.ca/~feldman/math/vble.pdf).

    

 If the error is greater than TOL, then the new step size for the iteration is

 

C is the constant of integration. SF is a safety factor (typically 0.9) that is used to ensure the new step does not overshoot the estimate.

The algorithm for adaptive step size Euler’s method can be thusly stated:

1)    % Define original step size (h), y_half and y_full, TOL – these are defined as part of the original Euler’s loop.
2)    Error = abs(y_half – y_full)
3)    Do Until Error <= TOL

-       Calculate hnew
-       Recalculate y_half and y_full with hnew

4)    Proceed to next time step

The example from Prof. Feldman’s notes was used to illustrate the concept. The IVP is:

 

A TOL of 0.005 was used for the analysis. The solution is shown in the figure below. Although the solutions for both the full and the half steps are practically the same with a 0.005 TOL, an interesting phenomenon can be observed at the circled locations in the figure. Is the “kink” real, or an artifact of the integration process?!

 

2-step Euler's method

One technique to improve the stability of the Euler’s method is to use a 2-step approach at each step of integration. That is, given a step size h, one can perform two sub-steps, t(n) to t(n+h/2) followed by t(n+h/2) to t(n+h). Mathematically, this becomes:



 The algorithm then becomes:
1)    % Define step size (h), initial function y(0), initial time t0, final time tf
2)    nosteps = (tf – t0)/h
3)    for i ← 1 to nosteps

-       Calculate derivative function f[t0,y[i-1]], and
-       y[i*] ← y[i-1] + 0.5*h* f[t0,y[i-1]]
-       t0 ← t0 + h/2
-       Calculate f[t0, y[i*]]
-       y[i] ← y[i*] + 0.5*h* f[t0, y[i*]]
-       t0 ← t0 + h

4)    % Display results

The example from Hairer & Lubich’s report (Numerical solution of ODE’s, source unknown) is a great example to illustrate this concept. The figure below shows the solution of the equation using a 1-step Euler method (with a step size of 0.038), and compares it with a 2-step solution. The 2-step solution has a more “smooth” behavior and hence a more stable. This is evident from the fact that the 2-step approach uses half the step size at each time step for the integration.

 


The 2-step Euler serves other practical uses too. Such an approach can be used to estimate the error in the solution (which can prove to be useful if an analytical solution is unknown). Based on this error at a particular step, the 2-step approach can potentially be used to modify the step size for future steps. This would pave way for an adaptive step size approach (contrast this with the existing approach which uses a fixed step size for all time steps).

Explicit vs Implicit Techniques

The Forward Euler's method presents an elegant technique to march from time tn to tn+1 using the knowledge of the solution at time tn. Methods that allow marching from one time step to the next in such a fashion are referred to as Explicit methods. The right hand side of the equation for an Explicit method does not have any quantities from the left hand side.

On the other hand, methods such as the Backward Euler require iterations at each step to converge at a solution. Such methods that require an iterative solution are referred to as Implicit methods. In Implicit methods, both sides of the equation have a common variable, which is the one to be solved.

The Trapezoidal Method

The Trapezoidal method of numerical integration is based on the premise that integration (which is the area under a curve) between two points on the abscissa can be approximated by a straight line between the corresponding ordinates. Mathematically, this can be represented as follows:

 

The similarity to the Backward Euler’s method is evident. The solution of the Trapezoidal method requires an iterative procedure at each time step to arrive at a solution for yn. A root-finding algorithm once again comes in handy for this iterative process.

A simplified algorithm for the Trapezoidal method can be:

1)    % Define step size (h), initial function y(0), initial time t0, final time tf, eps
2)    nosteps = (tf – t0)/h
3)    for i ← 1 to nosteps

- Calculate derivative function f[t0,y[i]]
- Iterate until y[i] – (y[i-1] + 0.5*h*{ f[x(i-1), y(i-1)] + f[x(i), y(i)]}) < eps
- t0 ← t0 + h

4)    % Display results

 Eq. 203(a) from J.C.Butcher, Numerical Solution of ODE’s, 2^nd Edition, was solved using the Trapezoidal method. The equations for the IVP are:

 

 

With y1(0)=1 and y2(0)= 0. A step size of 0.005, and eps of 1E-8 were used for the solver. The plots for y1 and y2 are shown below.

 

Backward Euler - part 2

The figure below shows the solution to the ODE from Curtiss & Hirschfelder, previously presented here. The figure below, however, was solved using the Backward Euler's method. The Backward Euler clearly has better convergence and stability compared to the Forward Euler. Irrespective of the step size 'h', the solutions clearly converge. The increase in calculation time from the iteration at each time step is made up for by the superior stability characteristics of this method.



So, which of the above solutions is now the "correct" one?!

The backward Euler's method

The examples in the previous post suggested the importance of step-size ‘h’ for numerical integration, and how improper choices of ‘h’ may lead to a divergent solution. The Euler’s method presented in the former post, as indicated earlier, marched from time tn to tn+1 using the knowledge of the solution at time tn. This method is also known as the Forward Euler, since it marches forward in time.

The forward Euler at time tn uses the derivative at tn to march to tn+1. Instead, if the derivative is obtained at time tn+1, the method becomes the Backward Euler. Mathematically, it is represented by the following equation:



Since the function y(x) appears on both sides of the equation, one can no longer simply march forward between time steps. Rather, one needs to perform an iterative root-finding algorithm to determine y(x) at each time step

A simplified algorithm for the Backward-Euler can be summarized as follows:

1)    % Define step size (h), initial function y(0), initial time t0, final time tf, eps
2)    nosteps = (tf – t0)/h
3)    for i ← 1 to nosteps

- Calculate derivative function f[t0,y[i]]
- Iterate until y[i] – (y[i-1] + h*f[x(i), y(i)]) < eps
- t0 ← t0 + h

4)    % Display results

‘eps’ is a user-specified tolerance value for the root-solver. The solver iterates until the equation at each time step is less than ‘eps’. The value that satisfies this condition is the numerical solution at that time. The iteration can be performed using any root-finding algorithm like the Bisection or the Newton-Raphson method. A modified form of the subroutine ‘rtbis’ adapted from Numerical Recipes, (The art of scientific computing, Press et al, 2^nd ed.) was used for this exercise.

The Backward Euler’s method was applied to the following problem (Atkinson et al, Numerical Solution of Ordinary Differential Equations, Eg. 5.8).

 

 The solution is shown in fig. 1.

 

Euler’s method part 2- Does it work for all cases?

Let us now consider applying the Euler’s method to the problem described in Curtiss & Hirschfelder (Integration of stiff equations, Proc. of the Natl. Acad. Of Sciences, 1952, Vol. 38, pp 235-243). This is the first order DE described by the equation

 


The results of the numerical integration are shown in fig. (1) for various step sizes ‘h’, for the initial value y(0)= 1.

 

 Fig. (1): Solution of a quadratic equation for various 'h' values

Clearly the numerical solution changes for various step sizes. So which of the solution curves in fig. (1) is the “correct” solution? The simplistic marching scheme presented by the Euler’s method is clearly not “stable” for all values of step sizes. In other words, the Euler’s method does not converge to a solution for any value of ‘h’. A minimum value of ‘h’ is thus required for the numerical solutions to converge. Note on fig. (1) that the solutions tend to converge as ‘h’ decreases.


The quest for a numerical integration procedure for an ODE is thus to come up with one that is stable for any and every value of ‘h’. The forward-Euler method clearly does not appear to meet this criteria for certain types of DE’s.


To illustrate the point, the solution of the equation

 

 from Ernst Hairer & Christian Lubich, (paper titled Numerical Solution of Ordinary Differential Equations, reference unknown) for various values of ‘h’ is shown in fig. (2).

 

Fig (2): Solution for y'(x) = -50(y-cosx)

These two examples clearly illustrate the need for numerical integration techniques that can converge to a solution independent of the step size ‘h’.

The Euler's Method

Given a differential equation of the form  , a curious mind (the kind of mind that has nothing better to do in life) may wonder how one can go about solving such a DE to produce a variety of colorful numerical results. A simple closed-form analytical solution would obviously be ideal to make things simple. However, let us assume for the moment that an analytical solution either does not exist, or cannot be determined. In most real world cases, this is a perfectly valid assumption. So, how does one go about numerically solving the above differential equation?


Perhaps the simplest of numerical integration techniques is the Euler’s method. The premise of the Euler method is based on the definition of the slope of a curve at a given point from basic calculus.




 

Rearranging the above eqn., one can obtain


 

The newly rearranged equation above represents a method for marching from stage ‘x’ to ‘x+h’, given a value for y’(x) at x=0. In other words, given f(0), one can march along from y(0) with incrementing values of h to obtain a numerical solution for the 1^st order ODE. Thus,


Step 0: f(0) = initial value
Step 1: f(step=1) = f(step=0) + hf’(step=0)
Step 2: f(step=2) = f(step=1) + hf’(step=1)
...

The recursive statements are usually represented in the following format:

 

The algorithm for Euler's method of numerical integration can be summarized as follows:


1) % Define step size (h), initial function y(0), initial time t0, final time tf
2) nosteps = (tf – t0)/h
3) for i ← 1 to nosteps

- Calculate derivative function f[t0,y[i]]
- y[i] ← y[i-1] + h*f[x,y]
- t0 ← t0 + h

4) % Display results

To illustrate the procedure, the Euler’s method was applied to the following initial value problem (Butcher, Numerical methods for ordinary differential equations, 201(a)) with a step size of 0.001.

 

 The result of the integrated function is plotted in fig. (1).

 

 

Visualizing differential equations

The solution of a differential equation (DE) can be obtained either analytically or numerically. Although analytical closed-form solutions are straight-forward and easy to comprehend, there exist a large variety of DE’s that cannot be solved analytically. One has to thus resort to numerical techniques to solve these problems.

Direction Fields serve as a valuable tool to visualize differential equations. In the simplest form, the derivative of a function at a specific location, say (x,y), is the slope of the function at that point. Consider, for example, the simple DE

 y’ = y (t), with boundary condition of y(0) = 1

 The above equation can be easily solved using well known techniques to obtain an analytical solution. Instead, let us attempt to plot the slope (i.e., y’) at various instances of time t, for various values of y. One such plot is shown below in Fig. (1). The direction fields provide a visual clue to the form of the solution for the initial value problem. Also plotted in Fig. 1 is the analytical solution (solid brown line).

 



Fig 1: Direction fields for y’ = y, with analytical solution y(t) = exp(t)

A variety of curves (i.e., solutions to the DE) can be visualized from Fig. 1. Each of these curves corresponds to their equivalent initial value problems. The analytical solution shown in Fig. 1 is one case of the initial value problem, where y(0)=1. Using the direction fields, one can visualize the form of the solution for various initial values. For a negative intercept on the ordinate (i.e., initial value problems with y(0) < 0), the form of the solution would be a mirror image of the solid brown line about the abscissa. This is visually evident from the direction fields shown for times t < 0 in Fig. 1.

Fig. 2 shows another example of a direction field plotted for the following 1^st order DE (Atkinson et al, Numerical Solution of Ordinary Differential Equations, problem 1(a))

y’ = -y(t) + sin(t) + cos(t), y(0) = 1

 

Fig. 2: Direction fields for y’ = -y + sin(t) + cos(t), with analytical solution